Educação: Aprenda a resolver equações do segundo grau usando a fórmula matemática Bhaskara

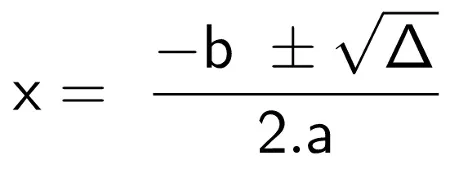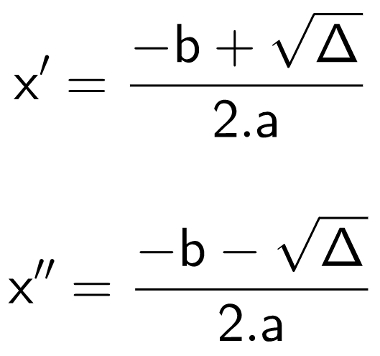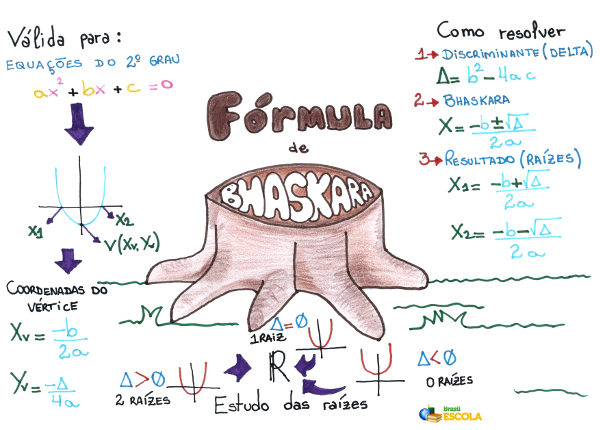
A fórmula de Bhaskara é um método resolutivo para equações do segundo grau cujo nome homenageia o grande matemático indiano que a demonstrou. Essa fórmulanada mais é do que um método para encontrar as raízes reais de uma equação do segundo grau fazendo uso apenas de seus coeficientes. Vale lembrar que coeficiente é o número que multiplica uma incógnita em uma equação.

Em sua forma original, a fórmula de Bhaskara é dada pela seguinte expressão:

Para utilizar essa fórmula, é necessário lembrar que toda equação do segundo grau deve ser escrita da seguinte maneira:

Equação reduzida ou normal do segundo grau

Os coeficientes dessa equação são os números que ocupam o lugar de “a”, de “b” e de “c”. Portanto, o coeficiente “a” é o número que multiplica x²; o coeficiente “b” é o número que multiplica x; e o coeficiente “c” é o número que não multiplica incógnita.

Como resolver equações do segundo grau com a fórmula de Bhaskara?

Resolver uma equação do segundo grau é encontrar os valores de x (ou da incógnita proposta) que fazem com que essa equação seja igual a zero.

O método resolutivo de Bhaskara apenas exige que o valor numérico de cada coeficiente seja substituído na fórmula de Bhaskara. Após isso, basta realizar as operações matemáticas indicadas pela fórmula para obter as raízes da equação. Contudo, esse método costuma ser dividido em três etapas para facilitar a compreensão por parte dos alunos.

Etapa 1: Calcular discriminante

Discriminante é a expressão presente dentro da raiz na fórmula de Bhaskara. É comumente representado pela letra grega Δ (Delta) e recebe esse nome pelo fato de discriminar os resultados de uma equação da seguinte maneira:

Δ < 0, então a equação não possui resultados reais;

Δ = 0, então a equação possui apenas um resultado real ou possui dois resultados iguais (essas duas afirmações são equivalentes);

Δ > 0, então a equação possui dois resultados distintos reais.

Portanto, para calcular as raízes de uma equação do segundo grau, primeiramente calcule o valor numérico de Δ.

Etapa 2: Substitua discriminante e coeficientes na fórmula de Bhaskara

Geralmente a fórmula de Bhaskara é ensinada apenas da seguinte maneira:

Nessa etapa, basta substituir os valores de Δ e dos coeficientes da equação do segundo grau na fórmula acima.

Etapa 3: Calcule as raízes da equação

Para essa última etapa, note na fórmula de Bhaskara que existe um sinal “±”. Esse sinal indica que devem ser realizados dois cálculos. O primeiro para o caso em que o número que o segue seja positivo e o segundo para o caso em que o número que o segue seja negativo.

É comum nomear cada um desses resultados como x’ e x” ou x₁ e x₂. Observe:

X’ e x” são as raízes da equação do segundo grau pela fórmula de Bhaskara

Exemplos

Exemplo 1 – Calcule as raízes da equação x² + 12x – 13 = 0.

Utilizando a fórmula de Bhaskara, separe os coeficientes da equação e realize o primeiro passo.

a = 1, b = 12 e c = – 13

Δ = b² – 4ac

Δ = 12² – 4·1·(– 13)

Δ = 144 + 52

Δ = 196

Tendo em mãos o valor de Δ, realize o segundo passo:

x = – b ± √Δ
2·a

x = – 12 ± √196
2·1

x = – 12 ± 14
2

Por fim, realize o terceiro passo para encontrar as raízes da equação do segundo grau.

x’ = – 12 + 14
2

x’ = 2
2

x’ = 1

x” = – 12 – 14
2

x” = – 26
2

x” = – 13

Portanto, as raízes da equação x² + 12x – 13 = 0 são 1 e – 13.

Exemplo 2 – Calcule as raízes da equação 2x² – 16x – 18 = 0

Utilizando a fórmula de Bhaskara, separe os coeficientes da equação e realize o primeiro passo.

a = 2, b = – 16 e c = – 18

Δ = b² – 4ac

Δ = (– 16)² – 4·2·(– 18)

Δ = 256 + 144

Δ = 400

Tendo em mãos o valor de Δ, realize o segundo passo:

x = – b ± √Δ
2·a

x = – (– 16) ± √400
2·2

x = 16 ± 20
4

Por fim, realize o terceiro passo para encontrar as raízes da equação do segundo grau:

x’ = 16 + 20
4

x’ = 36
4

x’ = 9

x” = 16 – 20
4

x” = – 4
4

x” = – 1

Portanto, as raízes da equação 2x² – 16x – 18 = 0 são 9 e – 1.

Por Luiz Paulo Moreira
Graduado em Matemática

(Fonte: Brasil Escola)